멀쩡한 사각형

작성일 | In

[프로그래머스] 멀쩡한 사각형

문제 링크

문제는 간단하지만 어떻게 풀어야 할지 고민이 필요한 문제였다.
직사각형의 대각선이 가로지르는 1x1 크기의 정사각형들이 총 몇개인지를 구해야 한다.
필자는 직사각형의 가로세로 비율 당 못쓰게된 정사각형의 개수에 초점을 맞췄다.

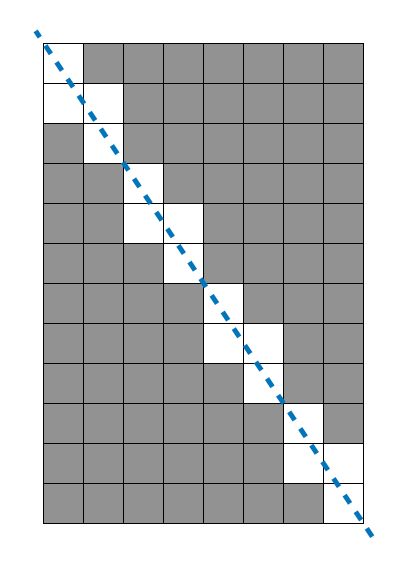
example-image

문제에 예시로 나와있는 그림을 보면, 일정한 비율로 못쓰게된 정사각형의 개수가 같음을 알 수 있다.
위 예시는 가로 8, 세로 12 크기의 직사각형이고, 이들의 가로세로 비율은 2:3이다. 가로 2, 세로 3의 미니 직사각형(?)을 기준으로 못쓰게된 정사각형이 4개가 발생함을 알 수 있다.
이를 일반화하면 못쓰게된 정사각형의 개수를 구하는 방법은 아래와 같다.

  1. 가로 w, 세로 h가 주어졌을 때 (w <= h), 가로세로 비 w:h를 가장 간단히 만든 a:b를 구한다.
  2. 가로 a, 세로 b인 직사각형에서 발생하는 못쓰게된 정사각형의 개수는 a + b - 1개이다.
  3. 가로 a, 세로 b인 직사각형이 전체 직사각형에서 몇 묶음이 있는지는 w / a를 통해 구할 수 있다. p = w / a라 할 때, 못쓰게된 정사각형의 개수는 p * (a + b - 1)개이다. (a는 w의 약수이므로 w % a는 항상 0이다.)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
using namespace std;

long long solution(int w,int h) {
    long long answer;
    
    if(w > h) {
        w ^= h; h ^= w; w ^= h;
    }

    long long dw=w, dh=h;
    int div=2;
    while(div <= dw) {
        if(dw % div == 0 && dh % div == 0) {
            dw /= div; dh /= div;
        } else
            ++div;
    }
    
    int p = w / dw;
    long long cut = p * (dh + dw - 1);

    answer = (long long)h * w - cut;

    return answer;
}

int main(void) {
    int a,b;
    cin >> a >> b;
    cout << solution(a,b);
}

규칙을 찾아내서 문제를 푸는데 한 한시간 정도 걸린 것 같다.
문제를 풀고 나서 다른 분들의 풀이를 보았는데, 최대공약수를 이용해서 아주 간단하게 푼 분의 풀이가 눈에 띄었다.
이 분은 직사각형에서 못쓰게된 정사각형의 개수를 h + w - GCD(h,w)로 구하셨는데, 어떻게 이것이 가능한지 이해하는데 시간이 좀 걸렸다. 생각해보니 결국 내가 푼 방식이 이 분의 풀이로 이어질 수 있음을 깨달았다.
필자의 코드에서 정답을 구하는 부분을 풀어서 살펴보면
answer = h x w - (p x (dw + dh - 1)) 이다. 이를 다시 풀어보면 h x w - p x dw - p x dh + p가 된다.
필자의 코드에서 p를 구하는 과정을 살펴보면, 결국 p는 w와 h의 GCD이고, dw와 dh는 w와 h를 GCD로 나눈 몫임을 알 수 있다.
즉, p x dw + p x dh - p = w + h - GCD와 같고, 이 문제는 주어진 직사각형의 가로, 세로 길이의 최대공약수로 풀 수 있음을 알 수 있다.

0%