저울

작성일 | In

[백준] 2437번 - 저울

문제 링크

KOI 2011 초등부 문제.
주어진 추를 오름차순 정렬한 뒤, 아래와 같은 아이디어를 이용하면 시간 내에 풀 수 있는 문제이다.

1
2
n개의 추들로 무게 1 ~ K를 표현할 수 있음이 보장되었을 때, 
K + 1 >= weight[n+1] 가 성립하면 n+1번째까지의 추들로 무게 1 ~ (K + weight[n+1])를 표현할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;

vector<int> weight;

int main(void) {
    int n;
    scanf("%d", &n);

    weight.resize(n);
    for(int i=0; i<n; ++i)
        scanf("%d", &weight[i]);
    
    sort(weight.begin(), weight.end());

    int answer=1;
    for(int w : weight) {
        if(answer < w) break;
        answer += w;
    }
    printf("%d", answer);
}

원리를 잠깐 살펴보자.
알고리즘 흐름상, 만약 현재까지의 추로 무게 4를 측정할 수 있다면 무게 1, 2, 3도 측정할 수 있다는 뜻이다.
(무게 1부터 1씩 올려가며 검사하기 때문)

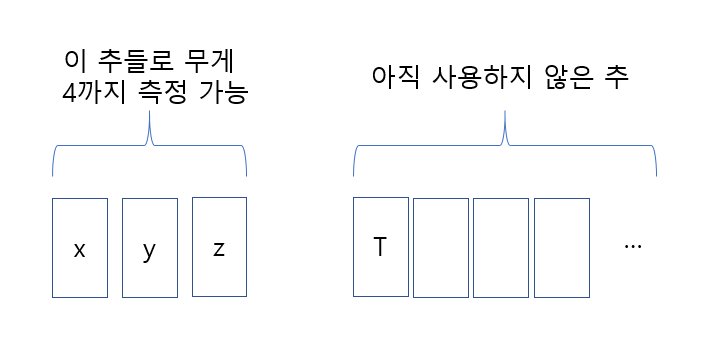
저울 예시 이미지

오름차순으로 추를 정렬해 두었기 때문에, 다음으로 사용할 추는 남은 추 중 가장 무게가 적은 추이다(이하 T).
만약 T의 무게가 5보다 작으면, x,y,z를 조합하여 무게 1,2,3,4를 만들 수 있으므로 무게 5를 반드시 측정할 수 있다.
만약 T의 무게가 5와 같다면, T 하나로 무게 5를 측정할 수 있다.
만약 T의 무게가 5보다 크다면 그 어느 조합으로도 무게 5를 측정할 수 없다.

0%