비트마스크

작성일 | In

[Algorithm] 비트마스크

비트마스크란?

어떤 상태나 상황을 비트열로 치환하여 십진수로 표현하는 방법을 말한다. 주로 집합의 상태를 쉽게 표현할 때 자주 쓰인다.

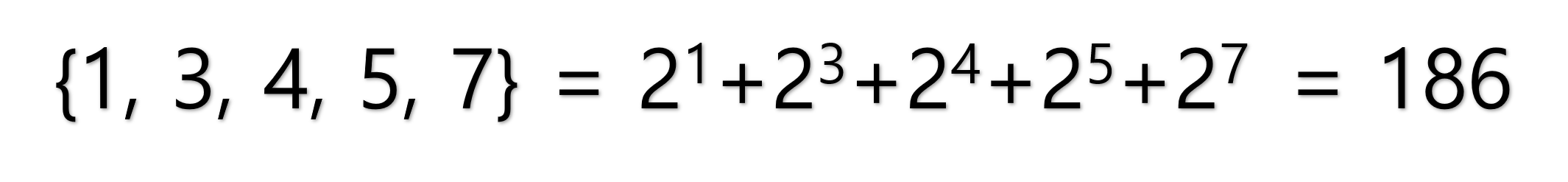
비트마스크 기본 예시

위 예시를 보자. 집합에서 어떠한 수는 존재하거나, 그렇지 않거나 2가지 상태일 수 있다. 즉, 모든 수의 상태는 이진수 비트열로 표현할 수 있다. 이 예시의 경우 10111010(2)으로 표현될 것이다. 이러한 비트열을 십진수로 바꾸면 186이 되고, 이 십진수를 이용한 코딩 방법이 비트마스크이다.

위를 보면 알 수 있듯이 비트마스크는 주로 상태를 표현하는데 자주 쓰이고, 특히 집합과 연관이 깊다. 이번엔 알고리즘 문제를 통해 정확히 어떻게 쓰이는지 그 느낌을 살펴보자.

백준 11723번 - 집합

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <cstdio>
#include <cstring>

int T;
int stat=0; // 집합 상태 표현할 변수

int main(void) {
    scanf("%d", &T);

    for(int i=0; i<T; i++) {
        char order[7];
        int num;

        scanf("%s", order);
        // all 명령과 empty 명령은 숫자를 받지 않으므로 따로 처리
        if(strcmp(order, "all") && strcmp(order, "empty")) scanf(" %d", &num);

        // 주어지는 num의 범위가 1 ~ 20 이므로 0번째 비트가 낭비된다.
        // 0번째 비트 ~ 19번째 비트를 사용하기 위해 num을 1 감소시켰다.
        num -= 1;

         // num을 2진수 비트열처럼 취급할 때 해당 비트열의 십진수 변환값을 저장한다.
        int numToBinary = (1<<num);

        if(order[0] == 'a' && order[1] == 'd') stat |= numToBinary;
        else if(order[0] == 'r') stat &= (~numToBinary);
        else if(order[0] == 'c') printf("%d\n", (stat & numToBinary) ? 1 : 0);
        else if(order[0] == 't') stat ^= numToBinary;
        else if(order[0] == 'a') stat = (1<<20) - 1;
        else stat = 0;
    }
}

우리가 코드에서 주목해야 할 부분은 if - else 구간에서의 비트 연산 방법이다. stat 변수가 어떻게 변화하는지 확인하기 위해 아래 예시를 통해 각 명령에 대한 결과를 살펴보자.

예시

add 1 , remove 2 , check 1 , toggle 4 , all , empty 순으로 명령이 주어졌다고 가정한다.

1.stat = 0(2), num = 0, numToBinary = 1(2) 이다. (stat |= numToBinary) 는 (stat = 0 | 1) 이고, 연산 결과 stat은 1(2)이 된다.

(stat |= (1«i)) 으로 i번째 비트를 켤 수 있다.
OR은 해당 비트가 켜져 있으면 그대로 두고, 꺼져 있으면 켜는 역할을 한다. 만약 여기서 + 연산을 한다면, 자릿수가 올라가 많은 비트가 변경되는 오류가 발생할 수 있다.

2.stat = 1(2), num = 1, numToBinary = 10(2) 이다. ~numToBinary = 01(2) 이고, 이를 stat과 AND 연산하면 stat = 01(2) 이다.

(stat &= ~(1«i)) 으로 i번째 비트를 끌 수 있다. 이 연산도 이미 꺼져 있는 비트는 그대로 유지한다. 만약 AND 대신 - 연산을 사용한다면 의도와는 다른 값으로 변할 수 있다는 점을 명심하자.

3.stat = 1(2), num = 0, numToBinary = 1(2) 이다. stat & numToBinary = 1(2) & 1(2) = 1(2) 즉, 1이 출력된다.

(stat & (1«i)) 으로 i번째 비트의 상태를 확인할 수 있다. 주의할 점은, 저 식의 결과값은 0 혹은 (1«i)이다. 만약 코드를 아래와 같이 짰다면 의도한 결과가 나오지 않는다. 조심하자.

1
2
3
4
5
6
// 0~9번째 비트 중 1의 갯수를 세는 코드. pending은 임의의 비트열이다.
// i = 3이고 pending의 3번쩨 비트가 켜져 있다면,
// pending & (1<<3) 는 1000(2), 즉 8을 반환하므로 count는 증가하지 않는다.
for(int i=0; i<10; i++) {
    if((pending & (1<<i)) == 1) ++count;
}

4.stat = 1(2), num = 3, numToBinary = 1000(2) 이다. stat과 numToBinary를 XOR 연산하면 stat = 1001(2) 가 된다.

(stat ^= (1«i)) 으로 i번째 비트를 반전시킬 수 있다.

5.(1«20) 은 길이가 21인 이진수 100….00(2) 이고, 여기서 1을 빼면 길이가 20인 이진수 111…11(2) 가 된다.

(stat = (1«p) - 1) 으로 길이가 p인 이진수의 모든 비트를 켤 수 있다.

0%